Congruent phase shift

function phi=coph(x1,x2)

% The congruent phase estimation between two signals
% with multiple frequencies and long length data > (N-1)*3+1
% x1 is the main (principle, foundamental) component
% phi is the congruent phase angle in Degrees
%
% © 2011 Michael Feldman
% For use with the book “HILBERT TRANSFORM APPLICATION
% IN MECHANICAL VIBRATION”, John Wiley & Sons, 2011

if length(x1)~=length(x2),disp(‘wrong length data’),return,end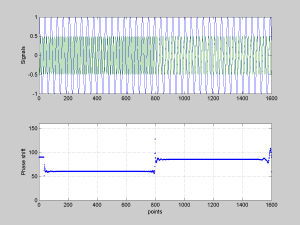
if length(x1)<=230*3,disp(‘too short data’),return,end
[A1,F1,phi1]=inst(x1,1);
[A2,F2,phi2]=inst(x2,1);
f1=lpf(F1,0.02);
f2=lpf(F2,0.02);

f1(f1==0)=eps; % avoid division by zero
r=round(f2./f1);
rd=diff(r);
ind=find(abs(rd)>=1)+1;
if isempty(ind)==1,seg_number=1; index=1:length(r);
m=round(mean(r(index))); x1i=cos(m*phi1(index));x2i=cos(phi2(index));
ph=phaseh(x1i,x2i);
else
seg_number=length(ind)+1;
for ii=1:seg_number
if ii==1, index=1:ind(ii)-1;
if length(index)<=230*3,ph{ii}=90.*ones(length(index),1);
else
m=round(mean(r(index)));x1i=cos(m*phi1(index));x2i=cos(phi2(index));
ph{ii}=phaseh(x1i,x2i);
end

elseif ii==seg_number,index=ind(ii-1):length(r);
if length(index)<=230*3,ph{ii}=90.*ones(length(index),1);
else
m=round(mean(r(index)));x1i=cos(m*phi1(index));x2i=cos(phi2(index));
ph{ii}=phaseh(x1i,x2i);
end

else index=ind(ii-1):ind(ii)-1;
if length(index)<=230*3,ph{ii}=90.*ones(length(index),1);
else
m=round(mean(r(index)));x1i=cos(m*phi1(index));x2i=cos(phi2(index));

ph{ii}=phaseh(x1i,x2i);
end

end
end
end
phi=[];
for jj=1:ii
phi=[phi; ph{jj}]; % congruent phase shift
end

return
% Example
clear
x1=[cos(0.15*(1:1600))’];
x2=[0.5*cos(0.45*(1:800)+60*pi/180)’; 0.5*cos(0.3*(801:1600)+85*pi/180)’];
phi=coph(x1,x2);
figure(1);
subplot(211)
plot([x1 x2])
ylabel(‘Signals’)
subplot(212)
plot(phi,’.’); grid on
axis([0 length(phi) 0 160]);
xlabel(‘points’)
ylabel(‘Phase shift’)