FORCEVIB (Matlab)

function [yy,A,f0,h,Ayd,f,m]=forcevib(x,y,Fs,stype);
% Function FORCEVIB (Forced Vibration Analysis)
% It determines instantaneous modal parameters of
% linear and non-linear vibration SDOF system under forced
% quasiharmonic excitation input.
% Input:
% Vector y is a forced vibration signal in time domain,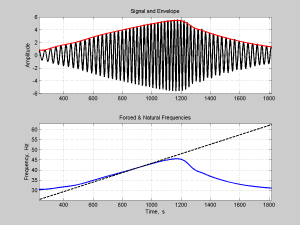
% Vector x is an input force excitation,
% stype is a signal type, e.g. displacement, velocity, or acceleration.
% Fs is the sampling frequency [Hz] %
% Output:
% yy – displacement, A – envelope, f0 – natural frequency [Hz],
% h – damping coefficient [1/sec],Ayd – envelope of the velocity,
% f – instantaneous frequency [Hz], m – mass value
%
% m*y” + 2*m*h*y’ +m*(2*pi*f0)^2*y = x
%
% EXAMPLE:
% [yy,A,f0,h,Ayd,f,m]=forcevib(x,y,1000,’d’);
%
% LIMITATIONS:
% The sampling frequency Fs has to be in the range Fs=(10-100)*f0.

% The minimum of points in time domain is 3*230+1.
%
% © 2011 Michael Feldman
% For use with the book “HILBERT TRANSFORM APPLICATION
% IN MECHANICAL VIBRATION”, John Wiley & Sons, 2011
%
N=230;

if length(y)<=3*N+1, error(‘The length of the signal y must be more than three times the filter order’),end;
if nargin<4, error(‘Not enough input arguments’), end;
if length(y)~=length(x), error(‘The length of the signal y must be equal to the length of the force excitation’),end;

s=strmatch(lower(stype),{‘displacement’,’velocity’,’acceleration’});
if s==0,error(‘Wrong signal type’);

y=y(:);

elseif s==1,
yH = hilbfir(y); % Displacement Hilbert transform
yd = diffir(y,Fs); % Velocity

ydd = diffir(yd,Fs); % Aceleration
yHd = hilbfir(yd); % Hilbert velocity
yHdd= hilbfir(ydd); % Hilbert aceleration

elseif s==2
yd = y; % Velocity
y = integ(yd,Fs); % Displacement
yH = hilbfir(y); % Displacement Hilbert transform
ydd = diffir(yd,Fs); % Aceleration
yHd = hilbfir(yd); % Hilbert velocity
yHdd= hilbfir(ydd); % Hilbert aceleration

elseif s==3
ydd=y; % Acceleration
yd = integ(ydd,Fs); % Velocity
y = integ(yd,Fs); % Displacement
yH = hilbfir(y); % Displacement Hilbert transform
yHd = hilbfir(yd); % Hilbert velocity
yHdd= hilbfir(ydd); % Hilbert aceleration

end

yy=y;

xH = hilbfir(x); % Force Hilbert
xd = diffir(x,Fs); % Force derivative
xHd = diffir(xH,Fs); % Force Hilbert derivative

% Algebraic transforms and instantaneous modal parameters calculation.
A2=(yH.^2+y.^2); A=sqrt(A2); % A — Vibration amplitude,
var2=(y.*yHd-yd.*yH);
om_y=var2./A2; % om_y — Vibration frequency,[rad]

var4=(-y.*ydd-yH.*yHdd); %%??
om0_2=(yHdd.*yd-yHd.*ydd)./(var2+eps); % om_02 — Undamped natural frequency, transient [rad] h0=0.5*(yH.*ydd-yHdd.*y)./(var2+eps); % h0 — Damping coefficient, transient [1/s] Ad_A_om=(y.*yd+yH.*yHd)./(var2+eps); %
Ayd2=(yHd.^2+yd.^2); Ayd=sqrt(Ayd2); % Ayd — Velocity amplitude,

Ax2=(xH.^2+x.^2); Ax=sqrt(Ax2); % A — Force amplitude,
alpha= (x.*y+xH.*yH)./(A2+eps); % Item of denominator of log.decrement,
beta = (xH.*y-x.*yH)./(A2+eps); % Item of numerator of log.decrement xHy-xyH
om_x = (x.*xHd-xH.*xd)./(Ax2+eps); % om_x — Vibration frequency,[rad] f=om_x/2/pi; om2=om_x.^2;

pp=233:length(y)-233;

[P,S]=polyfit(alpha(pp)-beta(pp).*Ad_A_om(pp),om0_2(pp),1);
m=1/P(1);

[As,inAs]=sort(A(pp)); % Sorting Amplitude
inAs=inAs+pp(1)-1;
dinAs=diff(inAs);

z=find(abs(dinAs)>200);
ppz=inAs(z);

if length(ppz)>=100; disp(‘PLEASE WAIT’)
options = optimset(‘Display’,’off’); % Optimization for Natural Frequency
m=-lsqnonlin(@omer,m,[],[],options);
end

om01_2=alpha./m-beta.*Ad_A_om/m+om0_2;
h=h0+0.5*A2.*beta./(var2+eps)./m;

% Low pass filtration (Result Smoothing)

fp=0.02;
f = lpf(f,fp); % Frequency [Hz]

A = lpf(A,fp); % Amplitude, Displaycement

f0 = sqrt(abs( lpf(om01_2,fp) ))/2/pi; % Natural frequency [Hz] h = lpf(h,fp); % Damping [1/s]

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function F = omer(m);
shift=20;
om01_2i=[];

er=[];

for i=1:length(ppz)-shift;
om01_2i=alpha(ppz(i:i+shift))./m-beta(ppz(i:i+shift)).*Ad_A_om(ppz(i:i+shift))/m-om0_2(ppz(i:i+shift));
er(i)=std(om01_2i);
end
F=er;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

returrn

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

load duffod
[yy,A,f0,h,Ayd,f,m]=forcevib(x,y,Fs,’d’);
plfor(yy,A,f0,h,Ayd,f,m);